Veri Madenciliği Dersi 6. Ünite Özet

Karar Ağaçları
Açıköğretim ders notları öğrenciler tarafından ders çalışma esnasında hazırlanmakta olup diğer ders çalışacak öğrenciler için paylaşılmaktadır. Sizlerde hazırladığınız ders notlarını paylaşmak istiyorsanız bizlere iletebilirsiniz.
Açıköğretim derslerinden Veri Madenciliği Dersi 6. Ünite Özet için hazırlanan ders çalışma dokümanına (ders özeti / sorularla öğrenelim) aşağıdan erişebilirsiniz. AÖF Ders Notları ile sınavlara çok daha etkili bir şekilde çalışabilirsiniz. Sınavlarınızda başarılar dileriz.
Karar Ağaçları
Giriş
Karar verme , karar vericinin karşılaştığı bir problem çözümünde olumlu bir sonuca ulaşabilmek için, problemin sunduğu birden fazla olası seçenek içerisinden seçim yapması işlemidir. Karar verme teknikleri en uygun kararın verilmesinde yardımcı olmak amacı ile geliştirilmiş tekniklerdir.
Karar probleminin zaman içerisinde doğuracağı sonuçlardan etkilenen sorumlu kişiye karar verici adı verilir. Karar verici için amaç , karar sürecinde önceden saptanan ve karar verici için belirgin özelliği olumlu olan sonuca ulaşmaktır. Çeşitli eylem seçenekleri arasından uygun olanını belirleyen kararın etkin olması ve bu kararı uygulayacak olanların arasında mümkün olduğu kadar yüksek düzeyde kabul görmesi beklenir. İyi bir karar, benzer problemler ile karşı karşıya kalan iki farklı yöneticinin aynı seçenekler ve aynı koşullar altında aynı kararı vermesi ile özdeşleştirilebilir. Karar probleminin karar vericinin karşısına çıkabilecek tüm sonuçları ya da senaryoları gösteren grafiksel bir yardımcı araca ihtiyacı olabilir. Karar ağaçları, karar vericinin içinde bulunduğu karar verme probleminde ortaya çıkabilecek tüm durumları ve karar vericinin karşılaşabileceği tüm senaryoları bir arada gösterebilen bir grafiksel yaklaşımdır.
Karar ağaçlarının bazı avantajları,
- Açıklanmalarının kolay olması,
- İnsani karar almayı diğer yaklaşımlara göre daha iyi yansıtması,
- Grafiksel olarak gösterilebilir olması,
- Uzman olmayan kişiler tarafından da kolaylıkla yorumlanabilir olması,
- Temsili değişkenlere ihtiyaç duymadan nitel değişkenleri de işleyebiliyor olmalarıdır.
Veri madenciliği uygulamalarında karar vericinin sıklıkla karşılaştığı problemlerden bir tanesi de sınıflandırma problemidir. Çok basit bir sınıflandırma örneği olarak, bir bankanın müşterilerini, müşterilerin çeşitli niteliklerini (gelir durumu, statüsü, borç durumu vb.) temel alarak, kredi uygunluk durumu gibi bir nitel değişkene göre riskli, risksiz olarak iki ayrı sınıfa gruplandırılması verilebilir. Sınıflandırma problemleri, veri madenciliğinde istatistiksel veya mantıksal yaklaşıma sahip yöntemler ile ele alınabilmektedir. Örneğin, diskriminant analizi sınıflandırma problemine matematiksel işlemler yardımıyla istatistiksel bir yaklaşım sağlar iken karar ağaçları, evet-hayır şeklinde değerlendirilen ifadeler ve karşılaştırma işlemleri yardımıyla mantıksal bir yaklaşım sağlar. Karar ağaçları, veri madenciliğinde karşılaşılan sınıflandırma problemlerinin çözümü için en sık başvurulan mantıksal yaklaşım yöntemidir.
Sınıflandırma , bir kaydı, önceden tanımlanmış çeşitli sınıflardan birine atayan bir modelin uygulanması işlemi olarak tanımlanabilir. Kestirim , bir rassal değişkenin seçtiğimiz modele göre parametrelerinin yerine konulması ile elde edilen değerdir. Sınıflandırma modeli ise, mevcut olan nitelik değerleri ile yeni bir kaydın sınıfının kestirimini yapar ve sınıflayıcı olarak adlandırılır.
Karar Ağaçları
Sınıflandırma tekniklerinden birisi de karar ağaçlarıdır. Problemde yer alan her bir nitelik için karar ağacında bir düğüm yer alır. Böylece niteliğin test edilmesi garanti altına alınır. Bir düğümden ayrılan dallar ise o düğümdeki testin tüm olası sonuçlarının her birine karşılık gelmektedir. Karar ağacının başlangıcını oluşturan ilk düğüm, kök düğüm olarak adlandırılır. Karar ağacı bu düğümden başlayarak, problemin içerisindeki tüm karar seçeneklerini içerecek şekilde düğümlerin mantık sırasına göre eklenmesiyle tamamlanır. Son düğüm, yaprak düğüm , diğer düğümler ise iç düğüm olarak adlandırılır. Yaprak düğümlerin her biri bir sınıfı temsil eder. Kimi sınıflandırma problemlerinde basit yapılı bir karar ağacı oluşurken, problemdeki nitelik sayısına bağlı olarak karar ağacı da karmaşık bir yapıya sahip olacaktır.
Bir bankanın, mevcut müşterilerini kredi risklerine göre sınıflamak istemesi durumunda borç, gelir, statü, risk seçeneklerine göre gruplaması ve örnek karar ağacı S.130-131’de incelenebilir .
Karar ağacının matematiksel çözümünü elde edebilmek için çeşitli tanımlamaların yapılmasına ihtiyaç vardır.
D = {t 1 , …, t n } veritabanını göstermek üzere, her t i t i =(t i1 ,t i2 ,…,t ih ) ise ve A = {A 1 , A 2 , …, A h } niteliklerini gösteriyor iken, C = {C 1 , C 2 , …, C m } sınıf kümesi olarak tanımlanmış olsun. D müşteri veritabanı ile ilişkilendirilen karar ağacı izleyen özelliklere sahip olacaktır:
- Her bir düğüm A i niteliği ile etiketlendirilecektir.
- Düğümden ayrılan her bir dal, ilgili düğüm ile ilişkili niteliğe uygulanabilen soru’nun yanıtlarıyla etiketlenecektir.
- Her bir yaprak düğüm C i sınıfıyla etiketlenecektir.
Karar ağaçlarını, sınıflandırma probleminin çözümlenmesinde kullanırken iki adıma ihtiyaç duyulur.
Bu adımlar,
- Karar ağacının oluşturulması
- Veritabanında yer alan her bir kaydın (t i ) sınıflandırmasının yapılması şeklindedir.
Karar ağacı oluşturulduktan sonra, her bir kayıt bu karar ağacının kök düğümden başlayarak, geçtiği her düğümdeki sorunun yönlendirmesine göre bir yaprak düğüme ulaşır ve böylece sınıflandırma işlemi tamamlanmış olur. Bu süreçte karşılaşılabilecek en önemli sorun, kök ve iç düğümlerde hangi niteliklerin yer alacağının tespit edilmesidir. Ayırma kriteri olarak öyle bir nitelik seçilmelidir ki diğer nitelikler ile karşılaştırıldığında en iyi ayırıcı nitelik olmalıdır. Nitelik bir kez belirlendikten sonra, kök düğümün temsil ettiği niteliğin test sonuçlarının her biri için dallar oluşturulur. Bu ayırma işlemi, karar ağacının büyümesi, örneğin bir düğümdeki kayıt sayısının bölünemeyecek kadar az olması veya ağaç derinliğinin araştırmacı tarafından belirlenen bir limite ulaşması gibi bir durma kriterine ulaşılana kadar devam edecektir.
Ayırma Kriterleri
Düğümün temsil ettiği, dolayısı ile ayırma işlemini en iyi şekilde gerçekleştirecek olan niteliğin seçilmesi için çeşitli ölçüler geliştirilmiştir. Bu ölçüler, niteliğin veri tipine göre değişiklik göstermektedir. Nitel veri için Entropi İndeksi, Gini İndeksi, Sınıflandırma Hatası İndeksi ve Twoing ölçüleri kullanılır. Ek olarak Twoing ölçüsünün sıralı ölçekle ölçülmüş değişkenlerin bulunduğu veri için Ordered Twoing bulunmaktadır. Nicel veriler için ise En Küçük Kareler Sapması yöntemi en sık kullanılan ölçüdür.
Entropi İndeksi ile En İyi Ayırıcı Niteliğin Seçilmesi
Entropi, bir veri yığınındaki düzensizliğin, rassallığın miktarını ölçmek için kullanılan bir ölçüdür. Veri yığını içinde, örneğin bankanın oluşturduğu müşteri veritabanındaki müşterileri sınıflayan kredi riski niteliğinde, tek bir sınıf olması durumunda, entropinin 0 (sıfır) olması beklenir. Çünkü bir düzensizlikten veya rassallıktan söz edilemez. Entropisi 0 olan bir grubun tam homojen bir grup, entropisi 1 olan grubun ise tam heterojen olduğu söylenebilir.
Bir veri yığınının, sınıflayıcı niteliğinin alacağı değerler C={C 1 , C 2 , …, C m } olmak üzere, m sınıfa ayırabilmesi için; ilgili sınıflar hakkında ortalama bilgiye ihtiyaç duyulacaktır. T sınıf değerlerini içeren küme iken, P T bu sınıfların olasılıklarını temsil etsin. Bu olasılık değerleri
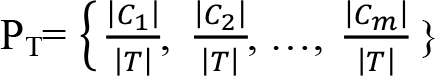
C i sınıfının T kümesindeki sayısını tespit edebilmek amacıyla |C i |’den yararlanılır. Bu durumda birinci sınıfın olasığı 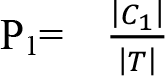 olacaktır. T için entropi hesabı yapılabilmesi için izleyen eşitlik kullanılır. H(T)=
olacaktır. T için entropi hesabı yapılabilmesi için izleyen eşitlik kullanılır. H(T)= ![]()
Entropi indeksi hesabını banka müşteri veritabanı örneği için S.133 incelenebilir.
T hedef niteliği, hedef niteliği olmayan bir X niteliğine bağlı olarak T 1 , T 2 , …, T m alt kümelerine ayrılmak istendiğinde, T’nin bir elemanının sınıfını belirleyebilmek için bilgiye ihtiyaç duyulur. Bu bilgi, T i ’nin bir elemanının sınıfının belirlenmesinde gerekli olan bilginin ağırlıklı ortalaması olarak kabul edilir. Hesaplanmanın gerçekleştirilmesi için izleyen eşitlik kullanılır.
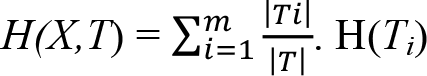
T hedef niteliğini X niteliğine göre bölerek elde edilen bilgiyi ölçmek için kazanç ölçütünden yararlanılır ve hesaplama için izleyen eşitlik kullanılır.
Kazanç(X, T) = H(T) ? H(X, T)
En yüksek kazancı sağlayan nitelik, ayırıcı nitelik olarak tanımlanır. Ancak, Entropi ve Gini indeksleri gibi indeksler belli değerleri çok sayıda bulunduran nitelikleri tercih etme eğilimindedirler. Benzer durumlarda kullanılan stratejilerden bir tanesi sadece ikili (binary) ayırma yapacak şekilde testler oluşturmak veya ayırmanın ne kadar iyi olduğunu belirlemek için kullanılan kazanç oranı ölçütünü kullanmaktır. Bu ölçüt, T’deki X’in bölünme bilgisinden yararlanmaktadır. Kazanç oranı ölçütün hesaplanması izleyen eşitlik yardımıyla yürütülür.
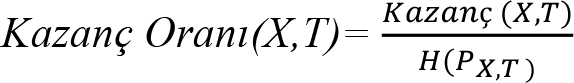
eşitlikte, (P X,T ), X değerlerinin olasılık dağılımını temsil etmektedir ve
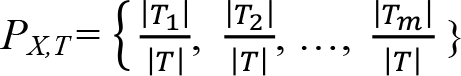
eşitliği yardımıyla hesaplanır. Bölünme bilgisi H(P X,T ) ise, 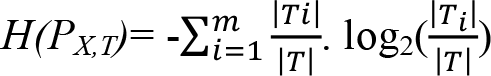 eşitliği ile hesaplanır.
eşitliği ile hesaplanır.
S.133 – 138’da bulunan örnek incelenebilir.
Gini İndeksi ve Ayırıcı Niteliğin Belirlenmesi
Gini indeksi, ikili bölünmeye dayanan bir tekniktir. Bu indeksin hesaplanmasında nitelik değerlerinin sola ve sağa olmak üzere iki bölüme ayrılması işlemi yürütülür. Gini indeksi hesaplanması için izlenecek adımlar;
1. Adım: Her nitelik değeri, sol ve sağ olmak üzere ikiye ayrılır, her bölüme karşılık gelen sınıf değerleri gruplandırılır.
2. Adım: Her bir niteliğin sol ve sağ tarafta yer alan bölünmeleri için Gini sol ve Gini sağ değerleri hesaplanır. Bu adımda kullanmak üzere hesaplanacak olan Gini indeks değerlerinin tespit edilmesi için izleyen eşitlikler kullanılır.
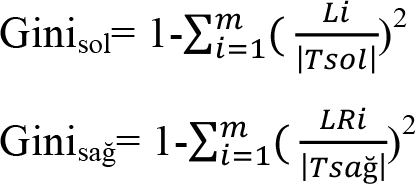
Eşitliklerde, m sınıf sayısını, T bir düğümdeki örnekleri, |T sol | ve |T sağ | sol taraftaki ve sağ taraftaki örnek sayılarını, L i ve R i ise sol ve sağ tarafta yer alan i kategorisindeki örnek sayılarını ifade etmektedir.
3. Adım: Her bir j niteliği için, n düğümdeki örnek sayısı iken, Gini indeksinin ağırlıklı ortalaması izleyen eşitlik yardımıyla hesaplanır:
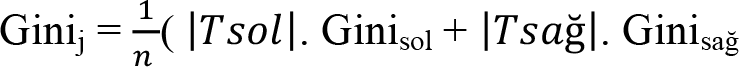
4. Adım : Her bir j niteliği için hesaplanan Gini j değerleri arasında en küçük olan seçilir, bölünme işlemi bu nitelik üzerinden gerçekleştirilir.
5. Adım: Bu adıma kadar yapılan tüm işlemler, karar ağacına yeni bir düğüm eklenemeyene kadar tekrarlanır.
Banka müşterileri veritabanı örneği borç, gelir ve statü nitelikleri ele alındığında, hangi niteliğin en iyi ayırıcı nitelik olduğunun Gini indeksi ile hesabı S:139-140’de incelenebilir.
Karar Ağacı Oluşturma Algoritmaları
Sınıflandırma problemlerinde bir karar ağacının oluşturulması için farklı algoritmalardan yararlanılabilir. Bu algoritmalara örnek olarak ID3, C4.5, CART, CHAID, QUEST, SLIQ, SPRINT ve MARS verilebilir. Bu algoritmalar, veri yığınını işleme şekline ve kullanılan ayırma kriterine göre değişiklik göstermektedir.
ID3 algoritması en basit karar ağacı oluşturma algoritmasıdır. Ayırma kriteri olarak kazanç ölçütünden yararlanılmaktadır. Karar ağacının büyümesini durdurma kriteri ise tüm kayıtların tek bir sınıfa ait olması veya kazanç ölçütünün sıfırdan büyük olmaması durumudur.
C4.5 algoritması , ID3 algoritmasının geliştirilmiş hâlidir. Ayırma kriteri olarak kazanç oranından yararlanılmaktadır. Karar ağacının büyümesini durdurma kriteri, ayrılacak olan kayıtların sayısının belirli bir eşiğin altına düşmesi durumudur. C4.5 algoritmasında, karar ağacının büyüme safhasından sonra, sınıflandırma hatasına dayanan budama işlemi uygulanmaktadır.
Kısaca CART olarak adlandırılan sınıflandırma ve regresyon ağaçları algoritması, ikili (binary) karar ağacı yapısından dolayı diğer algoritmalardan farklılık göstermektedir. Karar ağacındaki her bir düğüm yanlızca iki dala ayrılır. Ayırma kriteri için Entropi, Gini ve Twoing indekslerinden, karar ağacını budamak için ise maliyet karmaşıklığı kriterinden faydalanılır. CART algoritmasının önemli bir işlevi ise, yaprak düğümlerinde bir sınıf kestirimi yerine sayısal bir değer kestirimini içeren regresyon ağacının da oluşturulabilmesidir.
CHAID algoritması ilk olarak sayısal olmayan (ölçüm düzeyi sınıflayıcı) nitelikleri işleyebilecek şekilde geliştirilmiştir. CHAID algoritmasında, her girdi niteliği için, hedef niteliğe göre en az anlamlılıktaki farka sahip değer çiftleri bulur. CHAID algoritmasında, anlamlı olarak adlandırılan fark, istatistiksel bir testten elde edilen değeri ile ölçülür. Hedef, yani sınıf nitelik sürekli ise F testi, sınıflayıcı ise Pearson Ki-Kare testi, sıralayıcı ölçekle ölçülmüş ise maksimum benzerlik oranı testinden yararlanılmaktadır. CHAID algoritmasında, her seçilen değer çifti için elde edilen değerinin belli bir birleştirme eşik değerinden daha büyük olup olmadığı kontrol edilir ve olumlu sonuç alınan değerler doğru birleştirilir. Algoritma daha sonra da birleştirilebilecek potansiyel değer çiftleri aramaya devam eder. CHAID algoritmasında, oluşturulan karar ağacına budama uygulanmaz ve kayıp verinin söz konusu olması durumunda hepsini tek bir geçerli kategori olarak dikkate alarak işlem yürütülür.
QUEST algoritması , tek değişkenli ve doğrusal kombinasyon ayırmaları destekler. Her ayırma için (sıralayıcı veya sürekli niteliklerde) ANOVA F testi, Levene testi veya (sınıflayıcı niteliklerde) Pearson KiKare testi kullanılarak, girdi niteliklerinin her biri ile hedef yani sınıf niteliğinin arasındaki birliktelik hesaplanır. Eğer hedef nitelik çok terimli (multinominal) ise 2-ortalamalar kümeleme tekniği ile iki süper sınıf oluşturur. Hedef nitelik ile en yüksek birlikteliği elde eden girdi nitelik en iyi ayırıcı nitelik olarak seçilir. Oluşan ağaçları budamak için Tenfold çapraz doğrulama metodu kullanılır.
Karar Ağacı Budama Süreci ve Karar Ağacının Performansının Test Edilmesi
Budama bir ya da daha fazla dalı çıkartarak, karar ağacını daha basitleştirmek amacıyla, yaprak düğüm ile değiştirme işlemidir. Bu işlem, çıkartılmasına karar verilen dalın içerdiği kayıtların, bağlı olduğu üst düğüme dâhil edilerek, düğümün yaprak düğüme dönüştürülmesine dayanır. Böylece, kestirim hata oranının, ortaya çıkan aşırı uyum sorununun giderilmesi, azaltılması ve sınıflandırma modelinin kalitesinin arttırılması hedeflenir.
Budama süreci için çeşitli yöntemler geliştirilmiştir. Bu yöntemlerden bazıları maliyet karmaşıklığı, kötümser hata, hata-karmaşıklığı, kritik değer, azaltılmış hata, en küçük hata budama yöntemleridir.
Karar ağacı oluşturulurken, veritabanının bir kısmı modeli oluşturmak için kullanılırken, kalan kısım ise oluşturulan modelin test edilebilmesi için ayrılır. Veriyi ikiye ayırmanın amacı, kullanılan karar ağacı algoritmasının ortaya çıkardığı sınıflandırmanın test için saklanan veri ile tekrar denenerek, elde edilen sonuçlar arasında anlamlı bir farklılık olup olmadığının tespit edilmesidir. Bu amaca yönelik olarak kullanılan tekniklerden bazıları hold-out tekniği, tekrarlı hold-out tekniği , çapraz-doğrulama tekniği ve bootstrap tekniğidir .
Hold-out tekniği , veritabanının, araştırmacının takdirinde olan bir oranda (yarı yarıya veya 1/3’e 2/3 gibi) iki ayrık gruba bölünerek, eğitim ve test verisi olarak ele alınmasına dayanır.
Tekrarlı hold-out tekniği ise hold-out tekniğinin çoklu tekrarına dayanmaktadır. Toplam doğruluk, her bir tekrarda elde edilen model doğruluklarının aritmetik ortalaması olarak ifade edilir.
Çapraz-doğrulama yöntemind e ise, veritabanı iki eşit gruba bölünür ve birinci grup eğitim verisi olurken ikinci grup test verisi olarak ele alınır. Daha sonra, grupların rolleri değiştirilir. Modelin hatası, bu iki denemenin hataları toplamına eşittir. 2-katlı çapraz doğrulama olarak da adlandırılan bu yöntem, k-katlı olarak genelleştirilebilir. Bu durumda, veritabanı eşit büyüklükte k tane gruba bölünür.
Sınıflandırma ve Regresyon Ağaçlarının R Çözümü
Sınıflandırma ve regresyon ağaçları (CART), veri madenciliği sürecinde karşılaşılan sınıflandırma problemlerinde oldukça sık kullanılan bir yöntemdir. İkili (binary) karar ağaçları oluşturulduğu için diğer algoritmalardan ayrılmaktadır. Karar ağacındaki her bir düğüm sadece iki dala ayırır. Ayırma kriteri için Entropi, Gini ve Twoing indekslerinden, karar ağacını budamak için ise maliyet-karmaşıklığı kriterinden yararlanmaktadır. CART algoritmasının önemli bir işlevi ise, yaprak düğümlerinde bir sınıf kestirimi yerine sayısal bir değer kestirimini içeren regresyon ağacı da oluşturabilmesidir.
R’ye Veri Aktarma
R’ye veri aktarmanın birçok yöntemi mevcuttur. Bu yöntemlerden bazıları csv (comma seperated values) türü dosya ile veri aktarımı, kopyala-yapıştır yöntemi ve veritabanı bağlantısı ile veri aktarım yöntemidir.
csv Dosyası ile R’ye Veri Aktarma : csv dosya türü, günümüz veri işleme (işlem tablosu, veritabanı vb) uygulamalarının tümünde standart olarak kullanılan bir dosya türüdür. Birçok yazılım csv türü dosya oluşturma ve işleme yeteneklerine sahiptir. Herhangi bir yazılım kullanılarak, elinizdeki veri setinin csv dosya türünde kaydedilmesi gerekir. csv dosyası herhangi bir metin editörü ile bir kez açılarak, içeriğinin kontrol edilmesi yerinde olacaktır. Veritabanını csv dosya türünde kaydedebilmek için ilgili uygulamanın Dosya menüsünden Kaydet seçeneği kullanılarak kayıt işlemi gerçekleştirilir. S:14 Şekil 6.4 incelenebilir .
Aktarım için read.csv() fonksiyonundan yararlanılır. Bu fonksiyonun kullanımında gerekli olan parametreler file, header, sep ve dec parametreleridir. Diğer parametreler için R komut satırına help(read.csv) komutunu yazarak yardım alınabilir. file parametresi veri dosyasının kayıt ortamındaki konumunu ve dosya adını, header parametresi değişken isimlerinin ilk satırda olduğunu True değeri (yoksa False ) atanarak, sep parametresi ise veri noktalarını ayıran sembolün “,” olduğunu belirtmektedir. Dec parametresinin kullanımı, sayısal bir nitelik olmadığından gerekmemektedir. Eğer sayısal bir nitelik söz konusu olursa, ondalıklı sayının ondalık ayıracını ifade eden sembol bu parametre ile verilmelidir.
Kopyala-Yapıştır Komutu ile R’ye Veri Aktarma : Üzerinde çalışılan verinin küçük olması durumunda, veri aktarımı için tercih edilebilecek yöntem kopyala-yapıştır (Control+C/Control+V) yöntemidir. Bu yöntemde, öncelikle işlem tablosuna girilmiş olan verinin ihtiyaç duyulan kısmının kopyalanması gerekir. Seçme işleminden sonra işletim sisteminin uygun kopyalama tuş düzeni ile kopyalama işlemi gerçekleştirilir. Kopyalama işleminden sonra R uygulamasına geçiş yapılır. R’de read.table() fonksiyonu bu aşamada faydalı olacaktır. Bu fonksiyon için kullanılan parametreler read.csv komutu ile aynıdır. Ancak, kopyala-yapıştır yardımıyla veri aktarılacağı için file parametresi veri yolu yerine “clipboard” ifadesine sahip olacaktır, sep parametresi sekme anlamına gelen “t” ile kullanılacaktır. Komutun kullanımına dair detaylı bilgiler help(read.table) komutu ile elde edilebilir.
Veritabanı Erişimi ile R’ye Veri Aktarma : Bu bağlantı, Microsoft Windows işletim sisteminde yer alan ODBC (Open Database Connectivity) bağlantı türüdür. Bu bağlantı türü, farklı veritabanı sistemlerine standart teknikler ile bağlantı yapılmasını sağlar. Microsoft Windows işletim sisteminde, var olan bağlantıları öğrenmek veya yoksa bir bağlantı yaratmak için Denetim Masası -> Yönetimsel Araçlar -> Veri Kaynakları (ODBC) menü hiyerarşisi izlenebilir. R yazılımının, veritabanından veri alabilmesi için bu bağlantı türü de kullanılabilir. Ancak, bu işlemin gerçekleştirilebilmesi için ihtiyaç duyulan RODBC paketinin kurulu olması gerekmektedir. Paket Yükle seçeneği yardımıyla veya library(RODBC ) komutu yardımıyla RODBC paketi hafızaya yüklenebilir. Bu paketin, odbcConnect() ve sqlFetch() fonksiyonları yardımı ile bağlantı kurularak, veritabanındaki istenen bir veri tablosu okunabilir. odbcConnect() fonksiyonunun kullanımında gerekli olan parametreler dsn, uid ve pwd parametreleridir. Diğer parametreler için R komut satırına help(odbcConnect) komutunu yazarak yardım alınabilir. dsn parametresi sistemde kayıtlı olan veri kaynağının ismini, uid ve pwd parametreleri ise, veritabanına erişim için gerekli ise kullanıcı adı ve şifre değerlerini tanımlamaktadır.
Veri bağlantısı sağlandıktan sonra, sqlFetch() fonksiyonu yardımıyla istenen tabloya erişim sağlanır. sqlFetch() fonksiyonunun kullanımında gerekli olan parametreler channel ve sqtable parametreleridir.
Sınıflandırma ve Regresyon Ağaçlarının rpart Paketi ile Çözümü
rpart paketi içerisinde yer alan rpart() fonksiyonunda kullanılan parametreler sırasıyla, hedef niteliği de içeren herhangi bir etkileşimin söz konusu olmadığı ilişki formülünü ifade eden formula , formüldeki değişkenlerin çevrilebilmesi için gerekli olan veri yığınını içeren değişkeni ifade eden data v e karar ağacının oluşturulma amacını ifade eden method parametreleridir. Bu fonksiyon ile ilgili yardım için help(rpart) komutundan yararlanılabilir .
R ile elde edilen sınıflandırma ağacı modeli biraz daha detaylı incelenmek istenirse summary() fonksiyonundan yararlanılır . summary(agac) fonksiyonu yardımıyla detaylı olarak gösterilen sınıflandırma ağacı modeline göre, fonksiyonun ürettiği ilk tablo maliyet karmaşıklık parametrelerini içerir ve sınıflandırma ağacı için budama işlemi için gerekli görülüyorsa kullanılır.
Konu ile ilgili örnek S:149-154’de incelenebilir.
Giriş
Karar verme , karar vericinin karşılaştığı bir problem çözümünde olumlu bir sonuca ulaşabilmek için, problemin sunduğu birden fazla olası seçenek içerisinden seçim yapması işlemidir. Karar verme teknikleri en uygun kararın verilmesinde yardımcı olmak amacı ile geliştirilmiş tekniklerdir.
Karar probleminin zaman içerisinde doğuracağı sonuçlardan etkilenen sorumlu kişiye karar verici adı verilir. Karar verici için amaç , karar sürecinde önceden saptanan ve karar verici için belirgin özelliği olumlu olan sonuca ulaşmaktır. Çeşitli eylem seçenekleri arasından uygun olanını belirleyen kararın etkin olması ve bu kararı uygulayacak olanların arasında mümkün olduğu kadar yüksek düzeyde kabul görmesi beklenir. İyi bir karar, benzer problemler ile karşı karşıya kalan iki farklı yöneticinin aynı seçenekler ve aynı koşullar altında aynı kararı vermesi ile özdeşleştirilebilir. Karar probleminin karar vericinin karşısına çıkabilecek tüm sonuçları ya da senaryoları gösteren grafiksel bir yardımcı araca ihtiyacı olabilir. Karar ağaçları, karar vericinin içinde bulunduğu karar verme probleminde ortaya çıkabilecek tüm durumları ve karar vericinin karşılaşabileceği tüm senaryoları bir arada gösterebilen bir grafiksel yaklaşımdır.
Karar ağaçlarının bazı avantajları,
- Açıklanmalarının kolay olması,
- İnsani karar almayı diğer yaklaşımlara göre daha iyi yansıtması,
- Grafiksel olarak gösterilebilir olması,
- Uzman olmayan kişiler tarafından da kolaylıkla yorumlanabilir olması,
- Temsili değişkenlere ihtiyaç duymadan nitel değişkenleri de işleyebiliyor olmalarıdır.
Veri madenciliği uygulamalarında karar vericinin sıklıkla karşılaştığı problemlerden bir tanesi de sınıflandırma problemidir. Çok basit bir sınıflandırma örneği olarak, bir bankanın müşterilerini, müşterilerin çeşitli niteliklerini (gelir durumu, statüsü, borç durumu vb.) temel alarak, kredi uygunluk durumu gibi bir nitel değişkene göre riskli, risksiz olarak iki ayrı sınıfa gruplandırılması verilebilir. Sınıflandırma problemleri, veri madenciliğinde istatistiksel veya mantıksal yaklaşıma sahip yöntemler ile ele alınabilmektedir. Örneğin, diskriminant analizi sınıflandırma problemine matematiksel işlemler yardımıyla istatistiksel bir yaklaşım sağlar iken karar ağaçları, evet-hayır şeklinde değerlendirilen ifadeler ve karşılaştırma işlemleri yardımıyla mantıksal bir yaklaşım sağlar. Karar ağaçları, veri madenciliğinde karşılaşılan sınıflandırma problemlerinin çözümü için en sık başvurulan mantıksal yaklaşım yöntemidir.
Sınıflandırma , bir kaydı, önceden tanımlanmış çeşitli sınıflardan birine atayan bir modelin uygulanması işlemi olarak tanımlanabilir. Kestirim , bir rassal değişkenin seçtiğimiz modele göre parametrelerinin yerine konulması ile elde edilen değerdir. Sınıflandırma modeli ise, mevcut olan nitelik değerleri ile yeni bir kaydın sınıfının kestirimini yapar ve sınıflayıcı olarak adlandırılır.
Karar Ağaçları
Sınıflandırma tekniklerinden birisi de karar ağaçlarıdır. Problemde yer alan her bir nitelik için karar ağacında bir düğüm yer alır. Böylece niteliğin test edilmesi garanti altına alınır. Bir düğümden ayrılan dallar ise o düğümdeki testin tüm olası sonuçlarının her birine karşılık gelmektedir. Karar ağacının başlangıcını oluşturan ilk düğüm, kök düğüm olarak adlandırılır. Karar ağacı bu düğümden başlayarak, problemin içerisindeki tüm karar seçeneklerini içerecek şekilde düğümlerin mantık sırasına göre eklenmesiyle tamamlanır. Son düğüm, yaprak düğüm , diğer düğümler ise iç düğüm olarak adlandırılır. Yaprak düğümlerin her biri bir sınıfı temsil eder. Kimi sınıflandırma problemlerinde basit yapılı bir karar ağacı oluşurken, problemdeki nitelik sayısına bağlı olarak karar ağacı da karmaşık bir yapıya sahip olacaktır.
Bir bankanın, mevcut müşterilerini kredi risklerine göre sınıflamak istemesi durumunda borç, gelir, statü, risk seçeneklerine göre gruplaması ve örnek karar ağacı S.130-131’de incelenebilir .
Karar ağacının matematiksel çözümünü elde edebilmek için çeşitli tanımlamaların yapılmasına ihtiyaç vardır.
D = {t 1 , …, t n } veritabanını göstermek üzere, her t i t i =(t i1 ,t i2 ,…,t ih ) ise ve A = {A 1 , A 2 , …, A h } niteliklerini gösteriyor iken, C = {C 1 , C 2 , …, C m } sınıf kümesi olarak tanımlanmış olsun. D müşteri veritabanı ile ilişkilendirilen karar ağacı izleyen özelliklere sahip olacaktır:
- Her bir düğüm A i niteliği ile etiketlendirilecektir.
- Düğümden ayrılan her bir dal, ilgili düğüm ile ilişkili niteliğe uygulanabilen soru’nun yanıtlarıyla etiketlenecektir.
- Her bir yaprak düğüm C i sınıfıyla etiketlenecektir.
Karar ağaçlarını, sınıflandırma probleminin çözümlenmesinde kullanırken iki adıma ihtiyaç duyulur.
Bu adımlar,
- Karar ağacının oluşturulması
- Veritabanında yer alan her bir kaydın (t i ) sınıflandırmasının yapılması şeklindedir.
Karar ağacı oluşturulduktan sonra, her bir kayıt bu karar ağacının kök düğümden başlayarak, geçtiği her düğümdeki sorunun yönlendirmesine göre bir yaprak düğüme ulaşır ve böylece sınıflandırma işlemi tamamlanmış olur. Bu süreçte karşılaşılabilecek en önemli sorun, kök ve iç düğümlerde hangi niteliklerin yer alacağının tespit edilmesidir. Ayırma kriteri olarak öyle bir nitelik seçilmelidir ki diğer nitelikler ile karşılaştırıldığında en iyi ayırıcı nitelik olmalıdır. Nitelik bir kez belirlendikten sonra, kök düğümün temsil ettiği niteliğin test sonuçlarının her biri için dallar oluşturulur. Bu ayırma işlemi, karar ağacının büyümesi, örneğin bir düğümdeki kayıt sayısının bölünemeyecek kadar az olması veya ağaç derinliğinin araştırmacı tarafından belirlenen bir limite ulaşması gibi bir durma kriterine ulaşılana kadar devam edecektir.
Ayırma Kriterleri
Düğümün temsil ettiği, dolayısı ile ayırma işlemini en iyi şekilde gerçekleştirecek olan niteliğin seçilmesi için çeşitli ölçüler geliştirilmiştir. Bu ölçüler, niteliğin veri tipine göre değişiklik göstermektedir. Nitel veri için Entropi İndeksi, Gini İndeksi, Sınıflandırma Hatası İndeksi ve Twoing ölçüleri kullanılır. Ek olarak Twoing ölçüsünün sıralı ölçekle ölçülmüş değişkenlerin bulunduğu veri için Ordered Twoing bulunmaktadır. Nicel veriler için ise En Küçük Kareler Sapması yöntemi en sık kullanılan ölçüdür.
Entropi İndeksi ile En İyi Ayırıcı Niteliğin Seçilmesi
Entropi, bir veri yığınındaki düzensizliğin, rassallığın miktarını ölçmek için kullanılan bir ölçüdür. Veri yığını içinde, örneğin bankanın oluşturduğu müşteri veritabanındaki müşterileri sınıflayan kredi riski niteliğinde, tek bir sınıf olması durumunda, entropinin 0 (sıfır) olması beklenir. Çünkü bir düzensizlikten veya rassallıktan söz edilemez. Entropisi 0 olan bir grubun tam homojen bir grup, entropisi 1 olan grubun ise tam heterojen olduğu söylenebilir.
Bir veri yığınının, sınıflayıcı niteliğinin alacağı değerler C={C 1 , C 2 , …, C m } olmak üzere, m sınıfa ayırabilmesi için; ilgili sınıflar hakkında ortalama bilgiye ihtiyaç duyulacaktır. T sınıf değerlerini içeren küme iken, P T bu sınıfların olasılıklarını temsil etsin. Bu olasılık değerleri
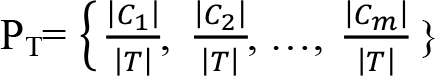
C i sınıfının T kümesindeki sayısını tespit edebilmek amacıyla |C i |’den yararlanılır. Bu durumda birinci sınıfın olasığı 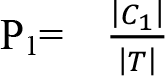 olacaktır. T için entropi hesabı yapılabilmesi için izleyen eşitlik kullanılır. H(T)=
olacaktır. T için entropi hesabı yapılabilmesi için izleyen eşitlik kullanılır. H(T)= ![]()
Entropi indeksi hesabını banka müşteri veritabanı örneği için S.133 incelenebilir.
T hedef niteliği, hedef niteliği olmayan bir X niteliğine bağlı olarak T 1 , T 2 , …, T m alt kümelerine ayrılmak istendiğinde, T’nin bir elemanının sınıfını belirleyebilmek için bilgiye ihtiyaç duyulur. Bu bilgi, T i ’nin bir elemanının sınıfının belirlenmesinde gerekli olan bilginin ağırlıklı ortalaması olarak kabul edilir. Hesaplanmanın gerçekleştirilmesi için izleyen eşitlik kullanılır.
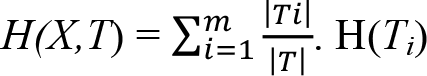
T hedef niteliğini X niteliğine göre bölerek elde edilen bilgiyi ölçmek için kazanç ölçütünden yararlanılır ve hesaplama için izleyen eşitlik kullanılır.
Kazanç(X, T) = H(T) ? H(X, T)
En yüksek kazancı sağlayan nitelik, ayırıcı nitelik olarak tanımlanır. Ancak, Entropi ve Gini indeksleri gibi indeksler belli değerleri çok sayıda bulunduran nitelikleri tercih etme eğilimindedirler. Benzer durumlarda kullanılan stratejilerden bir tanesi sadece ikili (binary) ayırma yapacak şekilde testler oluşturmak veya ayırmanın ne kadar iyi olduğunu belirlemek için kullanılan kazanç oranı ölçütünü kullanmaktır. Bu ölçüt, T’deki X’in bölünme bilgisinden yararlanmaktadır. Kazanç oranı ölçütün hesaplanması izleyen eşitlik yardımıyla yürütülür.
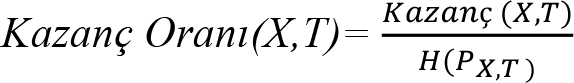
eşitlikte, (P X,T ), X değerlerinin olasılık dağılımını temsil etmektedir ve
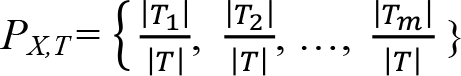
eşitliği yardımıyla hesaplanır. Bölünme bilgisi H(P X,T ) ise, 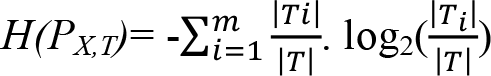 eşitliği ile hesaplanır.
eşitliği ile hesaplanır.
S.133 – 138’da bulunan örnek incelenebilir.
Gini İndeksi ve Ayırıcı Niteliğin Belirlenmesi
Gini indeksi, ikili bölünmeye dayanan bir tekniktir. Bu indeksin hesaplanmasında nitelik değerlerinin sola ve sağa olmak üzere iki bölüme ayrılması işlemi yürütülür. Gini indeksi hesaplanması için izlenecek adımlar;
1. Adım: Her nitelik değeri, sol ve sağ olmak üzere ikiye ayrılır, her bölüme karşılık gelen sınıf değerleri gruplandırılır.
2. Adım: Her bir niteliğin sol ve sağ tarafta yer alan bölünmeleri için Gini sol ve Gini sağ değerleri hesaplanır. Bu adımda kullanmak üzere hesaplanacak olan Gini indeks değerlerinin tespit edilmesi için izleyen eşitlikler kullanılır.
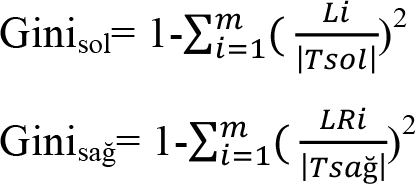
Eşitliklerde, m sınıf sayısını, T bir düğümdeki örnekleri, |T sol | ve |T sağ | sol taraftaki ve sağ taraftaki örnek sayılarını, L i ve R i ise sol ve sağ tarafta yer alan i kategorisindeki örnek sayılarını ifade etmektedir.
3. Adım: Her bir j niteliği için, n düğümdeki örnek sayısı iken, Gini indeksinin ağırlıklı ortalaması izleyen eşitlik yardımıyla hesaplanır:
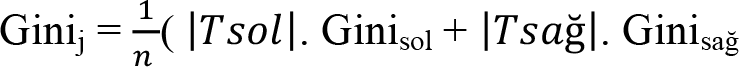
4. Adım : Her bir j niteliği için hesaplanan Gini j değerleri arasında en küçük olan seçilir, bölünme işlemi bu nitelik üzerinden gerçekleştirilir.
5. Adım: Bu adıma kadar yapılan tüm işlemler, karar ağacına yeni bir düğüm eklenemeyene kadar tekrarlanır.
Banka müşterileri veritabanı örneği borç, gelir ve statü nitelikleri ele alındığında, hangi niteliğin en iyi ayırıcı nitelik olduğunun Gini indeksi ile hesabı S:139-140’de incelenebilir.
Karar Ağacı Oluşturma Algoritmaları
Sınıflandırma problemlerinde bir karar ağacının oluşturulması için farklı algoritmalardan yararlanılabilir. Bu algoritmalara örnek olarak ID3, C4.5, CART, CHAID, QUEST, SLIQ, SPRINT ve MARS verilebilir. Bu algoritmalar, veri yığınını işleme şekline ve kullanılan ayırma kriterine göre değişiklik göstermektedir.
ID3 algoritması en basit karar ağacı oluşturma algoritmasıdır. Ayırma kriteri olarak kazanç ölçütünden yararlanılmaktadır. Karar ağacının büyümesini durdurma kriteri ise tüm kayıtların tek bir sınıfa ait olması veya kazanç ölçütünün sıfırdan büyük olmaması durumudur.
C4.5 algoritması , ID3 algoritmasının geliştirilmiş hâlidir. Ayırma kriteri olarak kazanç oranından yararlanılmaktadır. Karar ağacının büyümesini durdurma kriteri, ayrılacak olan kayıtların sayısının belirli bir eşiğin altına düşmesi durumudur. C4.5 algoritmasında, karar ağacının büyüme safhasından sonra, sınıflandırma hatasına dayanan budama işlemi uygulanmaktadır.
Kısaca CART olarak adlandırılan sınıflandırma ve regresyon ağaçları algoritması, ikili (binary) karar ağacı yapısından dolayı diğer algoritmalardan farklılık göstermektedir. Karar ağacındaki her bir düğüm yanlızca iki dala ayrılır. Ayırma kriteri için Entropi, Gini ve Twoing indekslerinden, karar ağacını budamak için ise maliyet karmaşıklığı kriterinden faydalanılır. CART algoritmasının önemli bir işlevi ise, yaprak düğümlerinde bir sınıf kestirimi yerine sayısal bir değer kestirimini içeren regresyon ağacının da oluşturulabilmesidir.
CHAID algoritması ilk olarak sayısal olmayan (ölçüm düzeyi sınıflayıcı) nitelikleri işleyebilecek şekilde geliştirilmiştir. CHAID algoritmasında, her girdi niteliği için, hedef niteliğe göre en az anlamlılıktaki farka sahip değer çiftleri bulur. CHAID algoritmasında, anlamlı olarak adlandırılan fark, istatistiksel bir testten elde edilen değeri ile ölçülür. Hedef, yani sınıf nitelik sürekli ise F testi, sınıflayıcı ise Pearson Ki-Kare testi, sıralayıcı ölçekle ölçülmüş ise maksimum benzerlik oranı testinden yararlanılmaktadır. CHAID algoritmasında, her seçilen değer çifti için elde edilen değerinin belli bir birleştirme eşik değerinden daha büyük olup olmadığı kontrol edilir ve olumlu sonuç alınan değerler doğru birleştirilir. Algoritma daha sonra da birleştirilebilecek potansiyel değer çiftleri aramaya devam eder. CHAID algoritmasında, oluşturulan karar ağacına budama uygulanmaz ve kayıp verinin söz konusu olması durumunda hepsini tek bir geçerli kategori olarak dikkate alarak işlem yürütülür.
QUEST algoritması , tek değişkenli ve doğrusal kombinasyon ayırmaları destekler. Her ayırma için (sıralayıcı veya sürekli niteliklerde) ANOVA F testi, Levene testi veya (sınıflayıcı niteliklerde) Pearson KiKare testi kullanılarak, girdi niteliklerinin her biri ile hedef yani sınıf niteliğinin arasındaki birliktelik hesaplanır. Eğer hedef nitelik çok terimli (multinominal) ise 2-ortalamalar kümeleme tekniği ile iki süper sınıf oluşturur. Hedef nitelik ile en yüksek birlikteliği elde eden girdi nitelik en iyi ayırıcı nitelik olarak seçilir. Oluşan ağaçları budamak için Tenfold çapraz doğrulama metodu kullanılır.
Karar Ağacı Budama Süreci ve Karar Ağacının Performansının Test Edilmesi
Budama bir ya da daha fazla dalı çıkartarak, karar ağacını daha basitleştirmek amacıyla, yaprak düğüm ile değiştirme işlemidir. Bu işlem, çıkartılmasına karar verilen dalın içerdiği kayıtların, bağlı olduğu üst düğüme dâhil edilerek, düğümün yaprak düğüme dönüştürülmesine dayanır. Böylece, kestirim hata oranının, ortaya çıkan aşırı uyum sorununun giderilmesi, azaltılması ve sınıflandırma modelinin kalitesinin arttırılması hedeflenir.
Budama süreci için çeşitli yöntemler geliştirilmiştir. Bu yöntemlerden bazıları maliyet karmaşıklığı, kötümser hata, hata-karmaşıklığı, kritik değer, azaltılmış hata, en küçük hata budama yöntemleridir.
Karar ağacı oluşturulurken, veritabanının bir kısmı modeli oluşturmak için kullanılırken, kalan kısım ise oluşturulan modelin test edilebilmesi için ayrılır. Veriyi ikiye ayırmanın amacı, kullanılan karar ağacı algoritmasının ortaya çıkardığı sınıflandırmanın test için saklanan veri ile tekrar denenerek, elde edilen sonuçlar arasında anlamlı bir farklılık olup olmadığının tespit edilmesidir. Bu amaca yönelik olarak kullanılan tekniklerden bazıları hold-out tekniği, tekrarlı hold-out tekniği , çapraz-doğrulama tekniği ve bootstrap tekniğidir .
Hold-out tekniği , veritabanının, araştırmacının takdirinde olan bir oranda (yarı yarıya veya 1/3’e 2/3 gibi) iki ayrık gruba bölünerek, eğitim ve test verisi olarak ele alınmasına dayanır.
Tekrarlı hold-out tekniği ise hold-out tekniğinin çoklu tekrarına dayanmaktadır. Toplam doğruluk, her bir tekrarda elde edilen model doğruluklarının aritmetik ortalaması olarak ifade edilir.
Çapraz-doğrulama yöntemind e ise, veritabanı iki eşit gruba bölünür ve birinci grup eğitim verisi olurken ikinci grup test verisi olarak ele alınır. Daha sonra, grupların rolleri değiştirilir. Modelin hatası, bu iki denemenin hataları toplamına eşittir. 2-katlı çapraz doğrulama olarak da adlandırılan bu yöntem, k-katlı olarak genelleştirilebilir. Bu durumda, veritabanı eşit büyüklükte k tane gruba bölünür.
Sınıflandırma ve Regresyon Ağaçlarının R Çözümü
Sınıflandırma ve regresyon ağaçları (CART), veri madenciliği sürecinde karşılaşılan sınıflandırma problemlerinde oldukça sık kullanılan bir yöntemdir. İkili (binary) karar ağaçları oluşturulduğu için diğer algoritmalardan ayrılmaktadır. Karar ağacındaki her bir düğüm sadece iki dala ayırır. Ayırma kriteri için Entropi, Gini ve Twoing indekslerinden, karar ağacını budamak için ise maliyet-karmaşıklığı kriterinden yararlanmaktadır. CART algoritmasının önemli bir işlevi ise, yaprak düğümlerinde bir sınıf kestirimi yerine sayısal bir değer kestirimini içeren regresyon ağacı da oluşturabilmesidir.
R’ye Veri Aktarma
R’ye veri aktarmanın birçok yöntemi mevcuttur. Bu yöntemlerden bazıları csv (comma seperated values) türü dosya ile veri aktarımı, kopyala-yapıştır yöntemi ve veritabanı bağlantısı ile veri aktarım yöntemidir.
csv Dosyası ile R’ye Veri Aktarma : csv dosya türü, günümüz veri işleme (işlem tablosu, veritabanı vb) uygulamalarının tümünde standart olarak kullanılan bir dosya türüdür. Birçok yazılım csv türü dosya oluşturma ve işleme yeteneklerine sahiptir. Herhangi bir yazılım kullanılarak, elinizdeki veri setinin csv dosya türünde kaydedilmesi gerekir. csv dosyası herhangi bir metin editörü ile bir kez açılarak, içeriğinin kontrol edilmesi yerinde olacaktır. Veritabanını csv dosya türünde kaydedebilmek için ilgili uygulamanın Dosya menüsünden Kaydet seçeneği kullanılarak kayıt işlemi gerçekleştirilir. S:14 Şekil 6.4 incelenebilir .
Aktarım için read.csv() fonksiyonundan yararlanılır. Bu fonksiyonun kullanımında gerekli olan parametreler file, header, sep ve dec parametreleridir. Diğer parametreler için R komut satırına help(read.csv) komutunu yazarak yardım alınabilir. file parametresi veri dosyasının kayıt ortamındaki konumunu ve dosya adını, header parametresi değişken isimlerinin ilk satırda olduğunu True değeri (yoksa False ) atanarak, sep parametresi ise veri noktalarını ayıran sembolün “,” olduğunu belirtmektedir. Dec parametresinin kullanımı, sayısal bir nitelik olmadığından gerekmemektedir. Eğer sayısal bir nitelik söz konusu olursa, ondalıklı sayının ondalık ayıracını ifade eden sembol bu parametre ile verilmelidir.
Kopyala-Yapıştır Komutu ile R’ye Veri Aktarma : Üzerinde çalışılan verinin küçük olması durumunda, veri aktarımı için tercih edilebilecek yöntem kopyala-yapıştır (Control+C/Control+V) yöntemidir. Bu yöntemde, öncelikle işlem tablosuna girilmiş olan verinin ihtiyaç duyulan kısmının kopyalanması gerekir. Seçme işleminden sonra işletim sisteminin uygun kopyalama tuş düzeni ile kopyalama işlemi gerçekleştirilir. Kopyalama işleminden sonra R uygulamasına geçiş yapılır. R’de read.table() fonksiyonu bu aşamada faydalı olacaktır. Bu fonksiyon için kullanılan parametreler read.csv komutu ile aynıdır. Ancak, kopyala-yapıştır yardımıyla veri aktarılacağı için file parametresi veri yolu yerine “clipboard” ifadesine sahip olacaktır, sep parametresi sekme anlamına gelen “t” ile kullanılacaktır. Komutun kullanımına dair detaylı bilgiler help(read.table) komutu ile elde edilebilir.
Veritabanı Erişimi ile R’ye Veri Aktarma : Bu bağlantı, Microsoft Windows işletim sisteminde yer alan ODBC (Open Database Connectivity) bağlantı türüdür. Bu bağlantı türü, farklı veritabanı sistemlerine standart teknikler ile bağlantı yapılmasını sağlar. Microsoft Windows işletim sisteminde, var olan bağlantıları öğrenmek veya yoksa bir bağlantı yaratmak için Denetim Masası -> Yönetimsel Araçlar -> Veri Kaynakları (ODBC) menü hiyerarşisi izlenebilir. R yazılımının, veritabanından veri alabilmesi için bu bağlantı türü de kullanılabilir. Ancak, bu işlemin gerçekleştirilebilmesi için ihtiyaç duyulan RODBC paketinin kurulu olması gerekmektedir. Paket Yükle seçeneği yardımıyla veya library(RODBC ) komutu yardımıyla RODBC paketi hafızaya yüklenebilir. Bu paketin, odbcConnect() ve sqlFetch() fonksiyonları yardımı ile bağlantı kurularak, veritabanındaki istenen bir veri tablosu okunabilir. odbcConnect() fonksiyonunun kullanımında gerekli olan parametreler dsn, uid ve pwd parametreleridir. Diğer parametreler için R komut satırına help(odbcConnect) komutunu yazarak yardım alınabilir. dsn parametresi sistemde kayıtlı olan veri kaynağının ismini, uid ve pwd parametreleri ise, veritabanına erişim için gerekli ise kullanıcı adı ve şifre değerlerini tanımlamaktadır.
Veri bağlantısı sağlandıktan sonra, sqlFetch() fonksiyonu yardımıyla istenen tabloya erişim sağlanır. sqlFetch() fonksiyonunun kullanımında gerekli olan parametreler channel ve sqtable parametreleridir.
Sınıflandırma ve Regresyon Ağaçlarının rpart Paketi ile Çözümü
rpart paketi içerisinde yer alan rpart() fonksiyonunda kullanılan parametreler sırasıyla, hedef niteliği de içeren herhangi bir etkileşimin söz konusu olmadığı ilişki formülünü ifade eden formula , formüldeki değişkenlerin çevrilebilmesi için gerekli olan veri yığınını içeren değişkeni ifade eden data v e karar ağacının oluşturulma amacını ifade eden method parametreleridir. Bu fonksiyon ile ilgili yardım için help(rpart) komutundan yararlanılabilir .
R ile elde edilen sınıflandırma ağacı modeli biraz daha detaylı incelenmek istenirse summary() fonksiyonundan yararlanılır . summary(agac) fonksiyonu yardımıyla detaylı olarak gösterilen sınıflandırma ağacı modeline göre, fonksiyonun ürettiği ilk tablo maliyet karmaşıklık parametrelerini içerir ve sınıflandırma ağacı için budama işlemi için gerekli görülüyorsa kullanılır.
Konu ile ilgili örnek S:149-154’de incelenebilir.
